Stochastic reaction-diffusion modelling

Introduction

There is a fairly large literature on reaction-diffusion modelling using partial differential equations (PDEs). There is also a fairly large literature on stochastic modelling of coupled chemical reactions, which account for the discreteness of reacting species at low concentrations. There is some literature on combining the two, to form stochastic reaction-diffusion systems, but much less.

In this post we will look at one approach to the stochastic reaction-diffusion problem, based on an underlying stochastic process often described by the reaction diffusion master equation (RDME). We will start by generating exact realisations from this process using the spatial Gillespie algorithm, before switching to a continuous stochastic approximation often known as the spatial chemical Langevin equation (spatial CLE). For fine discretisations, this spatial CLE is just an explicit numerical scheme for an associated reaction-diffusion stochastic partial differential equation (SPDE), and we can easily contrast such SPDE dynamics with their deterministic PDE approximation. We will investigate using simulation, based on my Scala library, scala-smfsb, which accompanies the third edition of my textbook, Stochastic modelling for systems biology, as discussed in previous posts.

All of the code used to generate the plots and movies in this post is available in my blog repo, and is very simple to build and run.

The Lotka-Volterra reaction network

Exact simulation from the RDME

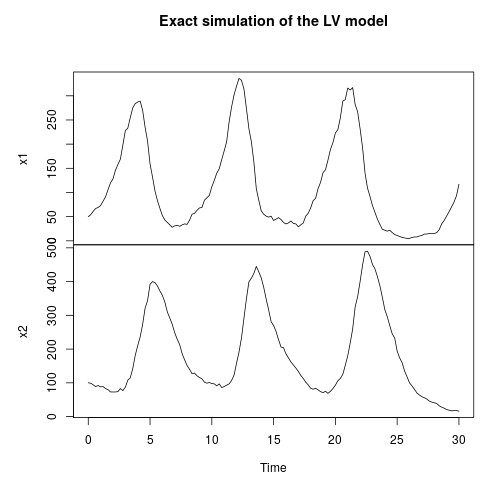
My favourite toy coupled chemical reaction network is the Lotka-Volterra predator-prey system, presented as the three reactions

with representing the prey species and the predator. I showed how to simulate realisations from this process using the Scala library in the previous post. Here we will consider simulation of this model in 2d, and simulate exact realisation from the appropriate RDME using the spatial Gillespie algorithm. Full runnable code for this simulation is here, but the key lines are:

val r = 100; val c = 120
val model = SpnModels.lv[IntState]()
val step = Spatial.gillespie2d(model, DenseVector(0.6, 0.6), maxH=1e12)
val x00 = DenseVector(0, 0)
val x0 = DenseVector(50, 100)
val xx00 = PMatrix(r, c, Vector.fill(r*c)(x00))
val xx0 = xx00.updated(c/2, r/2, x0)
val s = Stream.iterate(xx0)(step(_,0.0,0.1))

which sets up an infinite lazy Stream of states on a 100×120 grid over time steps of 0.1 units with diffusion rates of 0.6 for both species. We can then map this to a stream of images and visualise it using my scala-view library (described in this post). Running gives the following output:

The above image is the final frame of a movie which can be viewed by clicking on the image. In the simulation, blue represents the prey species, , and red represents the predator, . The simulation is initialised with a few prey and predators in the central pixel. At each time step of the simulation, either a reaction or a diffusion event may occur. If diffusion occurs, an individual moves from its current location to one of the four adjacent pixels. This algorithm is extremely computationally intensive, however well it is implemented. The implementation used here (using the function Spatial.gillespie2d in the scala-smfsb library) is quite inefficient. A more efficient implementation would use the next subvolume method or similar algorithm. But since every reaction event is simulated sequentially, this algorithm is always going to be intolerably slow for most interesting problems.

The spatial CLE

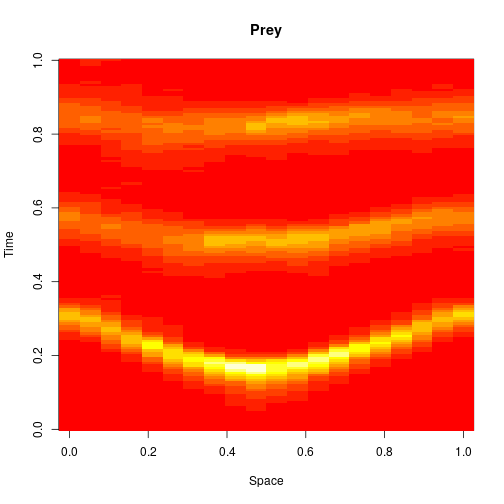
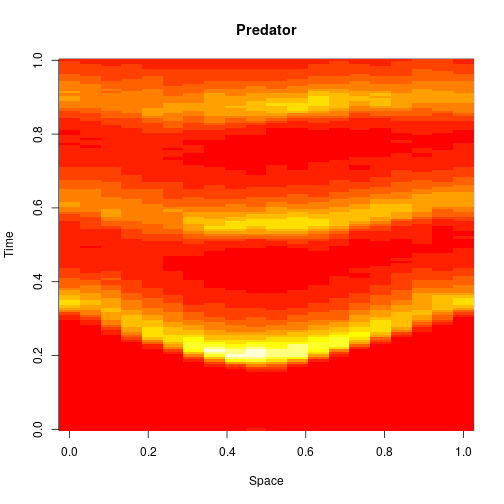
The spatial CLE effectively approximates the true RDME dynamics with a set of coupled stochastic differential equations (SDEs) on the spatial grid. This can be interpreted as an explicit scheme for numerically integrating an SPDE. But this numerical scheme is much more efficient, allowing sensible time-stepping of the process, and vectorises and parallelises nicely. The details are in my book, but the Scala implementation is here. Diffusion is implemented efficiently and in parallel using the comonadic approach that I’ve described previously. We can quickly and easily generate large simulations using the spatial CLE. Here is a movie generated on a 250×300 grid.

Again, clicking on the frame should give the movie. We see that although the quantitative details are slightly different to the exact algorithm, the essential qualitative behaviour of the system is captured well by the spatial CLE. Full code for this simulation is here.

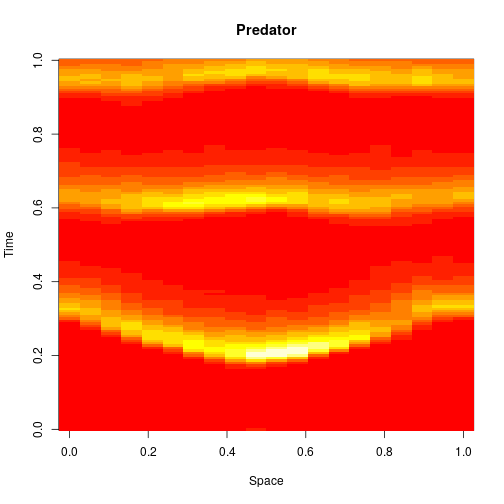
Reaction-diffusion PDE

If we remove all of the noise terms from the spatial CLE, we get a set of coupled ODEs, which again, may be interpreted as a numerical scheme for integrating a reaction-diffusion PDE model. Below are the dynamics on the same 250×300 grid.

It seems a bit harsh to describe a reaction-diffusion PDE as “boring”, but it certainly isn’t as interesting as the stochastic dynamics. Also, it has qualitatively quite different behaviour to the stochastic models, with wavefronts being less pronounced and less well separated. The code for this one is here.

Other initialisations

Instead of just seeding the simulation with some individuals in the central pixel, we can initialise 3 pixels. We can look first at a spatial CLE simulation.

Code here.

We can look at the same problem, but now using a PDE.

Code here.

Alternatively, we can initialise every pixel independently with random numbers of predator and prey. A movie for this is given below, following a short warm-up.

Code here.

Again, we can look at the corresponding deterministic integration.

Code here.

The SIR model

Let’s now turn attention to a spatial epidemic process model, the spatial susceptible-infectious-recovered model. Again, we’ll start from the discrete reaction formulation.

I’ll add this model to the next release of scala-smfsb, but in the meantime we can easily define it ourselves with:

def sir[S: State](p: DenseVector[Double] = DenseVector(0.1, 0.5)): Spn[S] =
  UnmarkedSpn[S](
    List("S", "I", "R"),
    DenseMatrix((1, 1, 0), (0, 1, 0)),
    DenseMatrix((0, 2, 0), (0, 0, 1)),
    (x, t) => {
      val xd = x.toDvd
      DenseVector(
        xd(0) * xd(1) * p(0), xd(1) * p(1)
      )}
  )

We can seed a simulation with a few infectious individuals in the centre of a roughly homogeneous population of susceptibles.

Spatial CLE

This time we’ll skip the exact simulation, since it’s very slow, and go straight to the spatial CLE. A simulation on a 250×300 grid is given below.

Here, green represents , red and blue . In this simulation, diffuses more slowly than , and doesn’t diffuse at all.
Code here.

PDE model

If we ditch the noise to get a reaction-diffusion PDE model, the dynamics are as follows.

Again, we see that the deterministic model is quite different to the stochastic version, and kind-of boring. Code here.

Further information

All of the code used to generate the plots and movies in this post is available in an easily runnable form in my blog repo. It is very easy to adapt the examples to vary parameters and initial conditions, and to study other reaction systems. Further details relating to stochastic reaction-diffusion modelling based on the RDME can be found in Chapter 9 of my textbook, Stochastic modelling for systems biology, third edition.

The smfsb R package

Introduction

In the previous post I gave a brief introduction to the third edition of my textbook, Stochastic modelling for systems biology. The algorithms described in the book are illustrated by implementations in R. These implementations are collected together in an R package on CRAN called smfsb. This post will provide a brief introduction to the package and its capabilities.

Installation

The package is on CRAN – see the CRAN package page for details. So the simplest way to install it is to enter

install.packages("smfsb")

at the R command prompt. This will install the latest version that is on CRAN. Once installed, the package can be loaded with

library(smfsb)

The package is well-documented, so further information can be obtained with the usual R mechanisms, such as

vignette(package="smfsb")
vignette("smfsb")
help(package="smfsb")
?StepGillespie
example(StepCLE1D)

The version of the package on CRAN is almost certainly what you want. However, the package is developed on R-Forge – see the R-Forge project page for details. So the very latest version of the package can always be installed with

install.packages("smfsb", repos="http://R-Forge.R-project.org")

if you have a reason for wanting it.

A brief tutorial

The vignette gives a quick introduction the the library, which I don’t need to repeat verbatim here. If you are new to the package, I recommend working through that before continuing. Here I’ll concentrate on some of the new features associated with the third edition.

Simulating stochastic kinetic models

Much of the book is concerned with the simulation of stochastic kinetic models using exact and approximate algorithms. Although the primary focus of the text is the application to modelling of intra-cellular processes, the methods are also appropriate for population modelling of ecological and epidemic processes. For example, we can start by simulating a simple susceptible-infectious-recovered (SIR) disease epidemic model.

set.seed(2)
data(spnModels)

stepSIR = StepGillespie(SIR)
plot(simTs(SIR$M, 0, 8, 0.05, stepSIR),
  main="Exact simulation of the SIR model")

The focus of the text is stochastic simulation of discrete models, so that is the obvious place to start. But there is also support for continuous deterministic simulation.

plot(simTs(SIR$M, 0, 8, 0.05, StepEulerSPN(SIR)),
  main="Euler simulation of the SIR model")

My favourite toy population dynamics model is the Lotka-Volterra (LV) model, so I tend to use this frequently as a running example throughout the book. We can simulate this (exactly) as follows.

stepLV = StepGillespie(LV)
plot(simTs(LV$M, 0, 30, 0.2, stepLV),
  main="Exact simulation of the LV model")

Stochastic reaction-diffusion modelling

The first two editions of the book were almost exclusively concerned with well-mixed systems, where spatial effects are ignorable. One of the main new features of the third edition is the inclusion of a new chapter on spatially extended systems. The focus is on models related to the reaction diffusion master equation (RDME) formulation, rather than individual particle-based simulations. For these models, space is typically divided into a regular grid of voxels, with reactions taking place as normal within each voxel, and additional reaction events included, corresponding to the diffusion of particles to adjacent voxels. So to specify such models, we just need an initial condition, a reaction model, and diffusion coefficients (one for each reacting species). So, we can carry out exact simulation of an RDME model for a 1D spatial domain as follows.

N=20; T=30
x0=matrix(0, nrow=2, ncol=N)
rownames(x0) = c("x1", "x2")
x0[,round(N/2)] = LV$M
stepLV1D = StepGillespie1D(LV, c(0.6, 0.6))
xx = simTs1D(x0, 0, T, 0.2, stepLV1D, verb=TRUE)
image(xx[1,,], main="Prey", xlab="Space", ylab="Time")

image(xx[2,,], main="Predator", xlab="Space", ylab="Time")

Exact simulation of discrete stochastic reaction diffusion systems is very expensive (and the reference implementation provided in the package is very inefficient), so we will often use diffusion approximations based on the CLE.

stepLV1DC = StepCLE1D(LV, c(0.6, 0.6))
xx = simTs1D(x0, 0, T, 0.2, stepLV1D)
image(xx[1,,], main="Prey", xlab="Space", ylab="Time")

image(xx[2,,], main="Predator", xlab="Space", ylab="Time")

We can think of this algorithm as an explicit numerical integration of the obvious SPDE approximation to the exact model.

The package also includes support for simulation of 2D systems. Again, we can use the Spatial CLE to speed things up.

m=70; n=50; T=10
data(spnModels)
x0=array(0, c(2,m,n))
dimnames(x0)[[1]]=c("x1", "x2")
x0[,round(m/2),round(n/2)] = LV$M
stepLV2D = StepCLE2D(LV, c(0.6,0.6), dt=0.05)
xx = simTs2D(x0, 0, T, 0.5, stepLV2D)
N = dim(xx)[4]
image(xx[1,,,N],main="Prey",xlab="x",ylab="y")

image(xx[2,,,N],main="Predator",xlab="x",ylab="y")

Bayesian parameter inference

Although much of the book is concerned with the problem of forward simulation, the final chapters are concerned with the inverse problem of estimating model parameters, such as reaction rate constants, from data. A computational Bayesian approach is adopted, with the main emphasis being placed on “likelihood free” methods, which rely on forward simulation to avoid explicit computation of sample path likelihoods. The second edition included some rudimentary code for a likelihood free particle marginal Metropolis-Hastings (PMMH) particle Markov chain Monte Carlo (pMCMC) algorithm. The third edition includes a more complete and improved implementation, in addition to approximate inference algorithms based on approximate Bayesian computation (ABC).

The key function underpinning the PMMH approach is pfMLLik, which computes an estimate of marginal model log-likelihood using a (bootstrap) particle filter. There is a new implementation of this function with the third edition. There is also a generic implementation of the Metropolis-Hastings algorithm, metropolisHastings, which can be combined with pfMLLik to create a PMMH algorithm. PMMH algorithms are very slow, but a full demo of how to use these functions for parameter inference is included in the package and can be run with

demo(PMCMC)

Simple rejection-based ABC methods are facilitated by the (very simple) function abcRun, which just samples from a prior and then carries out independent simulations in parallel before computing summary statistics. A simple illustration of the use of the function is given below.

data(LVdata)
rprior <- function() { exp(c(runif(1, -3, 3),runif(1,-8,-2),runif(1,-4,2))) }
rmodel <- function(th) { simTs(c(50,100), 0, 30, 2, stepLVc, th) }
sumStats <- identity
ssd = sumStats(LVperfect)
distance <- function(s) {
    diff = s - ssd
    sqrt(sum(diff*diff))
}
rdist <- function(th) { distance(sumStats(rmodel(th))) }
out = abcRun(10000, rprior, rdist)
q=quantile(out$dist, c(0.01, 0.05, 0.1))
print(q)

##       1%       5%      10% 
## 772.5546 845.8879 881.0573

accepted = out$param[out$dist < q[1],]
print(summary(accepted))

##        V1                V2                  V3         
##  Min.   :0.06498   Min.   :0.0004467   Min.   :0.01887  
##  1st Qu.:0.16159   1st Qu.:0.0012598   1st Qu.:0.04122  
##  Median :0.35750   Median :0.0023488   Median :0.14664  
##  Mean   :0.68565   Mean   :0.0046887   Mean   :0.36726  
##  3rd Qu.:0.86708   3rd Qu.:0.0057264   3rd Qu.:0.36870  
##  Max.   :4.76773   Max.   :0.0309364   Max.   :3.79220

print(summary(log(accepted)))

##        V1                V2               V3         
##  Min.   :-2.7337   Min.   :-7.714   Min.   :-3.9702  
##  1st Qu.:-1.8228   1st Qu.:-6.677   1st Qu.:-3.1888  
##  Median :-1.0286   Median :-6.054   Median :-1.9198  
##  Mean   :-0.8906   Mean   :-5.877   Mean   :-1.9649  
##  3rd Qu.:-0.1430   3rd Qu.:-5.163   3rd Qu.:-0.9978  
##  Max.   : 1.5619   Max.   :-3.476   Max.   : 1.3329

Naive rejection-based ABC algorithms are notoriously inefficient, so the library also includes an implementation of a more efficient, sequential version of ABC, often known as ABC-SMC, in the function abcSmc. This function requires specification of a perturbation kernel to “noise up” the particles at each algorithm sweep. Again, the implementation is parallel, using the parallel package to run the required simulations in parallel on multiple cores. A simple illustration of use is given below.

rprior <- function() { c(runif(1, -3, 3), runif(1, -8, -2), runif(1, -4, 2)) }
dprior <- function(x, ...) { dunif(x[1], -3, 3, ...) + 
    dunif(x[2], -8, -2, ...) + dunif(x[3], -4, 2, ...) }
rmodel <- function(th) { simTs(c(50,100), 0, 30, 2, stepLVc, exp(th)) }
rperturb <- function(th){th + rnorm(3, 0, 0.5)}
dperturb <- function(thNew, thOld, ...){sum(dnorm(thNew, thOld, 0.5, ...))}
sumStats <- identity
ssd = sumStats(LVperfect)
distance <- function(s) {
    diff = s - ssd
    sqrt(sum(diff*diff))
}
rdist <- function(th) { distance(sumStats(rmodel(th))) }
out = abcSmc(5000, rprior, dprior, rdist, rperturb,
    dperturb, verb=TRUE, steps=6, factor=5)

## 6 5 4 3 2 1

print(summary(out))

##        V1                V2               V3        
##  Min.   :-2.9961   Min.   :-7.988   Min.   :-3.999  
##  1st Qu.:-1.9001   1st Qu.:-6.786   1st Qu.:-3.428  
##  Median :-1.2571   Median :-6.167   Median :-2.433  
##  Mean   :-1.0789   Mean   :-6.014   Mean   :-2.196  
##  3rd Qu.:-0.2682   3rd Qu.:-5.261   3rd Qu.:-1.161  
##  Max.   : 2.1128   Max.   :-2.925   Max.   : 1.706

We can then plot some results with

hist(out[,1],30,main="log(c1)")

hist(out[,2],30,main="log(c2)")

hist(out[,3],30,main="log(c3)")

Although the inference methods are illustrated in the book in the context of parameter inference for stochastic kinetic models, their implementation is generic, and can be used with any appropriate parameter inference problem.

The smfsbSBML package

smfsbSBML is another R package associated with the third edition of the book. This package is not on CRAN due to its dependency on a package not on CRAN, and hence is slightly less straightforward to install. Follow the available installation instructions to install the package. Once installed, you should be able to load the package with

library(smfsbSBML)

This package provides a function for reading in SBML files and parsing them into the simulatable stochastic Petri net (SPN) objects used by the main smfsb R package. Examples of suitable SBML models are included in the main smfsb GitHub repo. An appropriate SBML model can be read and parsed with a command like:

model = sbml2spn("mySbmlModel.xml")

The resulting value, model is an SPN object which can be passed in to simulation functions such as StepGillespie for constructing stochastic simulation algorithms.

Other software

In addition to the above R packages, I also have some Python scripts for converting between SBML and the SBML-shorthand notation I use in the book. See the SBML-shorthand page for further details.

Although R is a convenient language for teaching and learning about stochastic simulation, it isn’t ideal for serious research-level scientific computing or computational statistics. So for the third edition of the book I have also developed scala-smfsb, a library written in the Scala programming language, which re-implements all of the models and algorithms from the third edition of the book in Scala, a fast, efficient, strongly-typed, compiled, functional programming language. I’ll give an introduction to this library in a subsequent post, but in the meantime, it is already well documented, so see the scala-smfsb repo for further details, including information on installation, getting started, a tutorial, examples, API docs, etc.

Source

This blog post started out as an RMarkdown document, the source of which can be found here.

Stochastic Modelling for Systems Biology, third edition

The third edition of my textbook, Stochastic Modelling for Systems Biology has recently been published by Chapman & Hall/CRC Press. The book has ISBN-10 113854928-2 and ISBN-13 978-113854928-9. It can be ordered from CRC Press, Amazon.com, Amazon.co.uk and similar book sellers.

I was fairly happy with the way that the second edition, published in 2011, turned out, and so I haven’t substantially re-written any of the text for the third edition. Instead, I’ve concentrated on adding in new material and improving the associated on-line resources. Those on-line resources are all free and open source, and hence available to everyone, irrespective of whether you have a copy of the new edition. I’ll give an introduction to those resources below (and in subsequent posts). The new material can be briefly summarised as follows:

• New chapter on spatially extended systems, covering the spatial Gillespie algorithm for reaction diffusion master equation (RDME) models in 1- and 2-d, the next subvolume method, spatial CLE, scaling issues, etc.
• Significantly expanded chapter on inference for stochastic kinetic models from data, covering approximate methods of inference (ABC), including ABC-SMC. The material relating to particle MCMC has also been improved and extended.
• Updated R package, including code relating to all of the new material
• New R package for parsing SBML models into simulatable stochastic Petri net models
• New software library, written in Scala, replicating most of the functionality of the R packages in a fast, compiled, strongly typed, functional language

New content

Although some minor edits and improvements have been made throughout the text, there are two substantial new additions to the text in this new edition. The first is an entirely new chapter on spatially extended systems. The first two editions of the text focused on the implications of discreteness and stochasticity in chemical reaction systems, but maintained the well-mixed assumption throughout. This is a reasonable first approach, since discreteness and stochasticity are most pronounced in very small volumes where diffusion should be rapid. In any case, even these non-spatial models have very interesting behaviour, and become computationally challenging very quickly for non-trivial reaction networks. However, we know that, in fact, the cell is a very crowded environment, and so even at small spatial scales, many interesting processes are diffusion limited. It therefore seems appropriate to dedicate one chapter (the new Chapter 9) to studying some of the implications of relaxing the well-mixed assumption. Entire books can be written on stochastic reaction-diffusion systems, so here only a brief introduction is provided, based mainly around models in the reaction-diffusion master equation (RDME) style. Exact stochastic simulation algorithms are discussed, and implementations provided in the 1- and 2-d cases, and an appropriate Langevin approximation is examined, the spatial CLE.

The second major addition is to the chapter on inference for stochastic kinetic models from data (now Chapter 11). The second edition of the book included a discussion of “likelihood free” Bayesian MCMC methods for inference, and provided a working implementation of likelihood free particle marginal Metropolis-Hastings (PMMH) for stochastic kinetic models. The third edition improves on that implementation, and discusses approximate Bayesian computation (ABC) as an alternative to MCMC for likelihood free inference. Implementation issues are discussed, and sequential ABC approaches are examined, concentrating in particular on the method known as ABC-SMC.

New software and on-line resources

Accompanying the text are new and improved on-line resources, all well-documented, free, and open source.

New website/GitHub repo

Information and materials relating to the previous editions were kept on my University website. All materials relating to this new edition are kept in a public GitHub repo: darrenjw/smfsb. This will be simpler to maintain, and will make it much easier for people to make copies of the material for use and studying off-line.

Updated R package(s)

Along with the second edition of the book I released an accompanying R package, “smfsb”, published on CRAN. This was a very popular feature, allowing anyone with R to trivially experiment with all of the models and algorithms discussed in the text. This R package has been updated, and a new version has been published to CRAN. The updates are all backwards-compatible with the version associated with the second edition of the text, so owners of that edition can still upgrade safely. I’ll give a proper introduction to the package, including the new features, in a subsequent post, but in the meantime, you can install/upgrade the package from a running R session with

install.packages("smfsb")

and then pop up a tutorial vignette with:

vignette("smfsb")

This should be enough to get you started.

In addition to the main R package, there is an additional R package for parsing SBML models into models that can be simulated within R. This package is not on CRAN, due to its dependency on a non-CRAN package. See the repo for further details.

There are also Python scripts available for converting SBML models to and from the shorthand SBML notation used in the text.

New Scala library

Another major new resource associated with the third edition of the text is a software library written in the Scala programming language. This library provides Scala implementations of all of the algorithms discussed in the book and implemented in the associated R packages. This then provides example implementations in a fast, efficient, compiled language, and is likely to be most useful for people wanting to use the methods in the book for research. Again, I’ll provide a tutorial introduction to this library in a subsequent post, but it is well-documented, with all necessary information needed to get started available at the scala-smfsb repo/website, including a step-by-step tutorial and some additional examples.

scala-glm: Regression modelling in Scala

Introduction

As discussed in the previous post, I’ve recently constructed and delivered a short course on statistical computing with Scala. Much of the course is concerned with writing statistical algorithms in Scala, typically making use of the scientific and numerical computing library, Breeze. Breeze has all of the essential tools necessary for building statistical algorithms, but doesn’t contain any higher level modelling functionality. As part of the course, I walked through how to build a small library for regression modelling on top of Breeze, including all of the usual regression diagnostics (such as standard errors, t-statistics, p-values, F-statistics, etc.). While preparing the course materials it occurred to me that it would be useful to package and document this code properly for general use. In advance of the course I packaged the code up into a bare-bones library, but since then I’ve fleshed it out, tidied it up and documented it properly, so it’s now ready for people to use.

The library covers PCA, linear regression modelling and simple one-parameter GLMs (including logistic and Poisson regression). The underlying algorithms are fairly efficient and numerically stable (eg. linear regression uses the QR decomposition of the model matrix, and the GLM fitting uses QR within each IRLS step), though they are optimised more for clarity than speed. The library also includes a few utility functions and procedures, including a pairs plot (scatter-plot matrix).

A linear regression example

Plenty of documentation is available from the scala-glm github repo which I won’t repeat here. But to give a rough idea of how things work, I’ll run through an interactive session for the linear regression example.

First, download a dataset from the UCI ML Repository to disk for subsequent analysis (caching the file on disk is good practice, as it avoids unnecessary load on the UCI server, and allows running the code off-line):

import scalaglm._
import breeze.linalg._

val url = "http://archive.ics.uci.edu/ml/machine-learning-databases/00291/airfoil_self_noise.dat"
val fileName = "self-noise.csv"

// download the file to disk if it hasn't been already
val file = new java.io.File(fileName)
if (!file.exists) {
  val s = new java.io.PrintWriter(file)
  val data = scala.io.Source.fromURL(url).getLines
  data.foreach(l => s.write(l.trim.
    split('\t').filter(_ != "").
    mkString("", ",", "\n")))
  s.close
}

Once we have a CSV file on disk, we can load it up and look at it.

val mat = csvread(new java.io.File(fileName))
// mat: breeze.linalg.DenseMatrix[Double] =
// 800.0    0.0  0.3048  71.3  0.00266337  126.201
// 1000.0   0.0  0.3048  71.3  0.00266337  125.201
// 1250.0   0.0  0.3048  71.3  0.00266337  125.951
// ...
println("Dim: " + mat.rows + " " + mat.cols)
// Dim: 1503 6
val figp = Utils.pairs(mat, List("Freq", "Angle", "Chord", "Velo", "Thick", "Sound"))
// figp: breeze.plot.Figure = breeze.plot.Figure@37718125

We can then regress the response in the final column on the other variables.

val y = mat(::, 5) // response is the final column
// y: DenseVector[Double] = DenseVector(126.201, 125.201, ...
val X = mat(::, 0 to 4)
// X: breeze.linalg.DenseMatrix[Double] =
// 800.0    0.0  0.3048  71.3  0.00266337
// 1000.0   0.0  0.3048  71.3  0.00266337
// 1250.0   0.0  0.3048  71.3  0.00266337
// ...
val mod = Lm(y, X, List("Freq", "Angle", "Chord", "Velo", "Thick"))
// mod: scalaglm.Lm =
// Lm(DenseVector(126.201, 125.201, ...
mod.summary
// Estimate	 S.E.	 t-stat	p-value		Variable
// ---------------------------------------------------------
// 132.8338	 0.545	243.866	0.0000 *	(Intercept)
//  -0.0013	 0.000	-30.452	0.0000 *	Freq
//  -0.4219	 0.039	-10.847	0.0000 *	Angle
// -35.6880	 1.630	-21.889	0.0000 *	Chord
//   0.0999	 0.008	12.279	0.0000 *	Velo
// -147.3005	15.015	-9.810	0.0000 *	Thick
// Residual standard error:   4.8089 on 1497 degrees of freedom
// Multiple R-squared: 0.5157, Adjusted R-squared: 0.5141
// F-statistic: 318.8243 on 5 and 1497 DF, p-value: 0.00000
val fig = mod.plots
// fig: breeze.plot.Figure = breeze.plot.Figure@60d7ebb0

There is a .predict method for generating point predictions (and standard errors) given a new model matrix, and fitting GLMs is very similar – these things are covered in the quickstart guide for the library.

Summary

scala-glm is a small Scala library built on top of the Breeze numerical library which enables simple and convenient regression modelling in Scala. It is reasonably well documented and usable in its current form, but I intend to gradually add additional features according to demand as time permits.

Statistical computing with Scala free on-line course

I’ve recently delivered a three-day intensive short-course on Scala for statistical computing and data science. The course seemed to go well, and the experience has convinced me that Scala should be used a lot more by statisticians and data scientists for a range of problems in statistical computing. In particular, the simplicity of writing fast efficient parallel algorithms is reason alone to take a careful look at Scala. With a view to helping more statisticians get to grips with Scala, I’ve decided to freely release all of the essential materials associated with the course: the course notes (as PDF), code fragments, complete examples, end-of-chapter exercises, etc. Although I developed the materials with the training course in mind, the course notes are reasonably self-contained, making the course quite suitable for self-study. At some point I will probably flesh out the notes into a proper book, but that will probably take me a little while.

I’ve written a brief self-study guide to point people in the right direction. For people studying the material in their spare time, the course is probably best done over nine weeks (one chapter per week), and this will then cover material at a similar rate to a typical MOOC.

The nine chapters are:

1. Introduction
2. Scala and FP Basics
3. Collections
4. Scala Breeze
5. Monte Carlo
6. Statistical modelling
7. Tools
8. Apache Spark
9. Advanced topics

For anyone frustrated by the limitations of dynamic languages such as R, Python or Octave, this course should provide a good pathway to an altogether more sophisticated, modern programming paradigm.

Stochastic Modelling for Systems Biology, second edition

The second edition of my textbook, Stochastic Modelling for Systems Biology was published on 7th November, 2011. One of the new features introduced into the new edition is an R package called smfsb which contains all of the code examples discussed in the text, which allow modelling, simulation and inference for stochastic kinetic models. The smfsb R package is the main topic of this post, but it seems appropriate to start off the post with a quick introduction to the book, and the main new features of the second edition.

The first edition was published in April 2006. It provided an introduction to mathematical modelling for systems biology from a stochastic viewpoint. It began with an introduction to biochemical network modelling, then moved on to probability theory, stochastic simulation and Markov processes. After providing all of the necessary background material, the book then introduced the theory of stochastic kinetic modelling and the Gillespie algorithm for exact discrete stochastic event simulation of stochastic kinetic biochemical network models. This was followed by examples and case studies, advanced simulation algorithms, and then a brief introduction to Bayesian inference and its application to inference for stochastic kinetic models.

The first edition proved to be very popular, as it was the first self-contained introduction to the field, and was aimed at an audience without a strong quantitative background. The decision to target an applied audience meant that it contained only the bare essentials necessary to get started with stochastic modelling in systems biology. The second edition was therefore an opportunity not only to revise and update the existing material, but also to add in additional material, especially new material which could provide a more solid foundation for advanced study by students with a more mathematical focus. New material introduced into the second edition includes a greatly expanded chapter on Markov processes, with particular emphasis on diffusion processes and stochastic differential equations, as well as Kolmogorov equations, the Fokker-Planck equation (FPE), Kurtz’s random time change representation of a stochastic kinetic model, an additional derivation of the chemical Langevin equation (CLE), and a derivation of the linear noise approximation (LNA). There is now also discussion of the modelling of “extrinsic” in addition to “intrinsic” noise. The final chapters on inference have also been greatly expanded, including discussion of importance resampling, particle filters, pseudo-marginal “exact approximate” MCMC, likelihood-free techniques and particle MCMC for rate parameter inference. I have tried as far as possible to maintain the informal and accessible style of the first edition, and a couple of the more technical new sections have been flagged as “skippable” by less mathematically trained students. In terms of computing, all of the SBML models have been updated to the new Level 3 specification, and all of the R code has been re-written, extended, documented and packaged as an open source R package. The rest of this post is an introduction to the R package. Although the R package is aimed mainly at owners of the second edition, it is well documented, and should therefore be usable by anyone with a reasonable background knowledge of the area. In particular, the R package should be very easy to use for anyone familiar with the first edition of the book. The introduction given here is closely based on the introductory vignette included with the package.

smfsb: an R package for simulation and inference in stochastic kinetic models

Overview

The smfsb package provides all of the R code associated with the book, Wilkinson (2011). Almost all of the code is pure R code, intended to be inspected from the R command line. In order to keep the code short, clean and easily understood, there is almost no argument checking or other boilerplate code.

Installation

The package is available from CRAN, and it should therefore be possible to install from the R command prompt using

install.packages("smfsb")

from any machine with an internet connection.

The package is being maintained on R-Forge, and so it should always be possible to install the very latest nightly build from the R command prompt with

install.packages("smfsb",repos="http://r-forge.r-project.org")

but you should only do this if you have a good reason to, in order not to overload the R-Forge servers (not that I imagine downloads of this package are likely to overload the servers…).

Once installed, the package can be loaded ready for use with

library(smfsb)

Accessing documentation

I have tried to ensure that the package and all associated functions and datasets are properly documented with runnable examples. So,

help(package="smfsb")

will give a brief overview of the package and a complete list of all functions. The list of vignettes associated with the package can be obtained with

vignette(package="smfsb")

At the time of writing, the introductory vignette is the only one available, and can be accessed from the R command line with

vignette("smfsb",package="smfsb")

Help on functions can be obtained using the usual R mechanisms. For example, help on the function StepGillespie can be obtained with

?StepGillespie

and the associated example can be run with

example(StepGillespie)

The sourcecode for the function can be obtained by typing StepGillespie on a line by itself. In this case, it returns the following R code:

function (N) 
{
    S = t(N$Post - N$Pre)
    v = ncol(S)
    return(function(x0, t0, deltat, ...) {
        t = t0
        x = x0
        termt = t0 + deltat
        repeat {
            h = N$h(x, t, ...)
            h0 = sum(h)
            if (h0 < 1e-10)
                t = 1e+99 
            else if (h0 > 1e+06) {
                t = 1e+99
                warning("Hazard too big - terminating simulation!")
            } 
            else 
                t = t + rexp(1, h0)
            if (t >= termt) 
                return(x)
            j = sample(v, 1, prob = h)
            x = x + S[, j]
        }
    })
}

A list of demos associated with the package can be obtained with

demo(package="smfsb")

A list of data sets associated with the package can be obtained with

data(package="smfsb")

For example, the small table, mytable from the introduction to R in Chapter 4 can by loaded with

data(mytable)

After running this command, the data frame mytable will be accessible, and can be examined by typing

mytable

at the R command prompt.

Simulation of stochastic kinetic models

The main purpose of this package is to provide a collection of tools for building and simulating stochastic kinetic models. This can be illustrated using a simple Lotka-Volterra predator-prey system. First, consider the prey, and the predator as a stochastic network, viz

The first “reaction” represents predator reproduction, the second predator-prey interaction and the third predator death. We can write the stoichiometries of the reactions, together with the rate (or hazard) of each reaction, in tabular form as

Reaction	Pre		Post		Hazard
	1	0	2	0
	1	1	0	2
	0	1	0	0

This can be encoded in R as a stochastic Petri net (SPN) using

# SPN for the Lotka-Volterra system
LV=list()
LV$Pre=matrix(c(1,0,1,1,0,1),ncol=2,byrow=TRUE)
LV$Post=matrix(c(2,0,0,2,0,0),ncol=2,byrow=TRUE)
LV$h=function(x,t,th=c(th1=1,th2=0.005,th3=0.6))
{
 with(as.list(c(x,th)),{
         return(c(th1*x1, th2*x1*x2, th3*x2 ))
        })
}

This object could be created directly by executing

data(spnModels)

since the LV model is one of the standard demo models included with the package. Functions for simulating from the transition kernel of the Markov process defined by the SPN can be created easily by passing the SPN object into the appropriate constructor. For example, if simulation using the Gillespie algorithm is required, a simulation function can be created with

stepLV=StepGillespie(LV)

This resulting function (closure) can then be used to advance the state of the process. For example, to simulate the state of the process at time 1, given an initial condition of , at time 0, use

stepLV(c(x1=50,x2=100),0,1)

Alternatively, to simulate a realisation of the process on a regular time grid over the interval [0,100] in steps of 0.1 time units, use

out = simTs(c(x1=50,x2=100),0,100,0.1,stepLV)
plot(out,plot.type="single",col=c(2,4))

which gives the resulting plot

See the help and runnable example for the function StepGillespie for further details, including some available alternative simulation algorithms, such as StepCLE.

Inference for stochastic kinetic models from time course data

Estimating the parameters of stochastic kinetic models using noisy time course measurements on some aspect of the system state is a very important problem. Wilkinson (2011) takes a Bayesian approach to the problem, using particle MCMC methodology. For this, a key aspect is the use of a particle filter to compute an unbiased estimate of marginal likelihood. This is accomplished using the function pfMLLik. Once a method is available for generating unbiased estimates for the marginal likelihood, this may be embedded into a fairly standard marginal Metropolis-Hastings algorithm for parameter estimation. See the help and runnable example for pfMLLik for further details, along with the particle MCMC demo, which can by run using demo(PMCMC). I’ll discuss more about particle MCMC and rate parameter inference in the next post.

References

Wilkinson, D. J. (2006) Stochastic Modelling for Systems Biology, Boca Raton, Florida: Chapman & Hall/CRC Press.

Wilkinson, D. J. (2011) Stochastic Modelling for Systems Biology, second edition, Boca Raton, Florida: Chapman & Hall/CRC Press.