The scala-smfsb library

In the previous post I gave a very quick introduction to the smfsb R package. As mentioned in that post, although good for teaching and learning, R isn’t a great language for serious scientific computing or computational statistics. So for the publication of the third edition of my textbook, Stochastic modelling for systems biology, I have created a library in the Scala programming language replicating the functionality provided by the R package. Here I will give a very quick introduction to the scala-smfsb library. Some familiarity with both Scala and the smfsb R package will be helpful, but is not strictly necessary. Note that the library relies on the Scala Breeze library for linear algebra and probability distributions, so some familiarity with that library can also be helpful.

Setup

To follow the along you need to have Sbt installed, and this in turn requires a recent JDK. If you are new to Scala, you may find the setup page for my Scala course to be useful, but note that on many Linux systems it can be as simple as installing the packages openjdk-8-jdk and sbt.

Once you have Sbt installed, you should be able to run it by entering sbt at your OS command line. You now need to use Sbt to create a Scala REPL with a dependency on the scala-smfsb library. There are many ways to do this, but if you are new to Scala, the simplest way is probably to start up Sbt from an empty or temporary directory (which doesn’t contain any Scala code), and then paste the following into the Sbt prompt:

set libraryDependencies += "com.github.darrenjw" %% "scala-smfsb" % "0.6"
set libraryDependencies += "org.scalanlp" %% "breeze-viz" % "0.13.2"
set scalaVersion := "2.12.6"
set scalacOptions += "-Yrepl-class-based"
console

The first time you run this it will take a little while to download and cache various library dependencies. But everything is cached, so it should be much quicker in future. When it is finished, you should have a Scala REPL ready to enter Scala code.

An introduction to scala-smfsb

It should be possible to type or copy-and-paste the commands below one-at-a-time into the Scala REPL. We need to start with a few imports.

import smfsb._
import breeze.linalg.{Vector => BVec, _}
import breeze.numerics._
import breeze.plot._

Note that I’ve renamed Breeze’s Vector type to BVec to avoid clashing with that in the Scala standard library. We are now ready to go.

Simulating models

Let’s begin by instantiating a Lotka-Volterra model, simulating a single realisation of the process, and then plotting it.

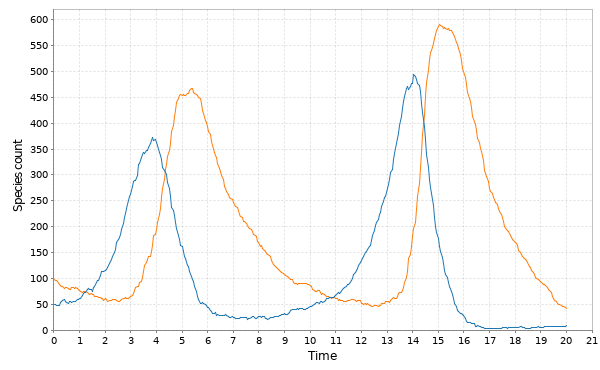
// Simulate LV with Gillespie
val model = SpnModels.lv[IntState]()
val step = Step.gillespie(model)
val ts = Sim.ts(DenseVector(50, 100), 0.0, 20.0, 0.05, step)
Sim.plotTs(ts, "Gillespie simulation of LV model with default parameters")

The library comes with a few other models. There’s a Michaelis-Menten enzyme kinetics model:

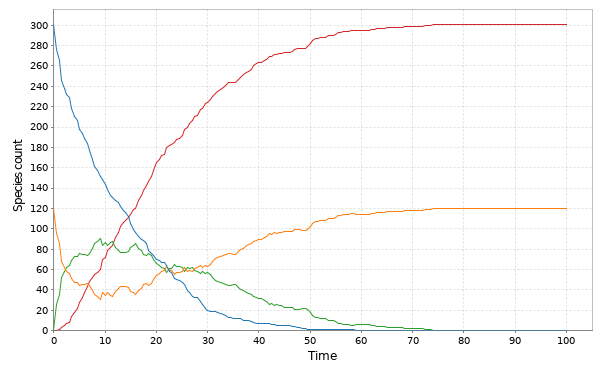
// Simulate other models with Gillespie
val stepMM = Step.gillespie(SpnModels.mm[IntState]())
val tsMM = Sim.ts(DenseVector(301,120,0,0), 0.0, 100.0, 0.5, stepMM)
Sim.plotTs(tsMM, "Gillespie simulation of the MM model")

and an auto-regulatory genetic network model, for example.

val stepAR = Step.gillespie(SpnModels.ar[IntState]())
val tsAR = Sim.ts(DenseVector(10, 0, 0, 0, 0), 0.0, 500.0, 0.5, stepAR)
Sim.plotTs(tsAR, "Gillespie simulation of the AR model")

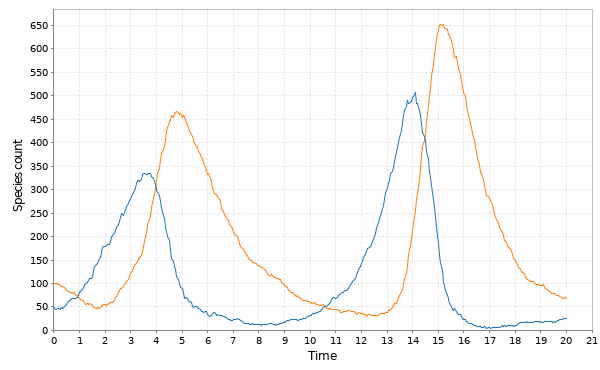
If you know the book and/or the R package, these models should all be familiar.
We are not restricted to exact stochastic simulation using the Gillespie algorithm. We can use an approximate Poisson time-stepping algorithm.

// Simulate LV with other algorithms
val stepPts = Step.pts(model)
val tsPts = Sim.ts(DenseVector(50, 100), 0.0, 20.0, 0.05, stepPts)
Sim.plotTs(tsPts, "Poisson time-step simulation of the LV model")

Alternatively, we can instantiate the example models using a continuous state rather than a discrete state, and then simulate using algorithms based on continous approximations, such as Euler-Maruyama simulation of a chemical Langevin equation (CLE) approximation.

val stepCle = Step.cle(SpnModels.lv[DoubleState]())
val tsCle = Sim.ts(DenseVector(50.0, 100.0), 0.0, 20.0, 0.05, stepCle)
Sim.plotTs(tsCle, "Euler-Maruyama/CLE simulation of the LV model")

If we want to ignore noise temporarily, there’s also a simple continuous deterministic Euler integrator built-in.

val stepE = Step.euler(SpnModels.lv[DoubleState]())
val tsE = Sim.ts(DenseVector(50.0, 100.0), 0.0, 20.0, 0.05, stepE)
Sim.plotTs(tsE, "Continuous-deterministic Euler simulation of the LV model")

Spatial stochastic reaction-diffusion simulation

We can do 1d reaction-diffusion simulation with something like:

val N = 50; val T = 40.0
val model = SpnModels.lv[IntState]()
val step = Spatial.gillespie1d(model,DenseVector(0.8, 0.8))
val x00 = DenseVector(0, 0)
val x0 = DenseVector(50, 100)
val xx00 = Vector.fill(N)(x00)
val xx0 = xx00.updated(N/2,x0)
val output = Sim.ts(xx0, 0.0, T, 0.2, step)
Spatial.plotTs1d(output)

For 2d simulation, we use PMatrix, a comonadic matrix/image type defined within the library, with parallelised map and coflatMap (cobind) operations. See my post on comonads for scientific computing for further details on the concepts underpinning this, though note that it isn’t necessary to understand comonads to use the library.

val r = 20; val c = 30
val model = SpnModels.lv[DoubleState]()
val step = Spatial.cle2d(model, DenseVector(0.6, 0.6), 0.05)
val x00 = DenseVector(0.0, 0.0)
val x0 = DenseVector(50.0, 100.0)
val xx00 = PMatrix(r, c, Vector.fill(r*c)(x00))
val xx0 = xx00.updated(c/2, r/2, x0)
val output = step(xx0, 0.0, 8.0)
val f = Figure("2d LV reaction-diffusion simulation")
val p0 = f.subplot(2, 1, 0)
p0 += image(PMatrix.toBDM(output map (_.data(0))))
val p1 = f.subplot(2, 1, 1)
p1 += image(PMatrix.toBDM(output map (_.data(1))))

Bayesian parameter inference

The library also includes functions for carrying out parameter inference for stochastic dynamical systems models, using particle MCMC, ABC and ABC-SMC. See the examples directory for further details.

Next steps

Having worked through this post, the next step is to work through the tutorial. There is some overlap of content with this blog post, but the tutorial goes into more detail regarding the basics. It also finishes with suggestions for how to proceed further.

Source

This post started out as a tut document (the Scala equivalent of an RMarkdown document). The source can be found here.