Introduction to parallel MCMC for Bayesian inference, using C, MPI, the GSL and SPRNG
Introduction
This post is aimed at people who already know how to code up Markov Chain Monte Carlo (MCMC) algorithms in C, but are interested in how to parallelise their code to run on multi-core machines and HPC clusters. I discussed different languages for coding MCMC algorithms in a previous post. The advantage of C is that it is fast, standard and has excellent scientific library support. Ultimately, people pursuing this route will be interested in running their code on large clusters of fast servers, but for the purposes of development and testing, this really isn’t necessary. A single dual-core laptop, or similar, is absolutely fine. I develop and test on a dual-core laptop running Ubuntu linux, so that is what I will assume for the rest of this post.
There are several possible environments for parallel computing, but I will focus on the Message-Passing Interface (MPI). This is a well-established standard for parallel computing, there are many implementations, and it is by far the most commonly used high performance computing (HPC) framework today. Even if you are ultimately interested in writing code for novel architectures such as GPUs, learning the basics of parallel computation using MPI will be time well spent.
MPI
The whole point of MPI is that it is a standard, so code written for one implementation should run fine with any other. There are many implementations. On Linux platforms, the most popular are OpenMPI, LAM, and MPICH. There are various pros and cons associated with each implementation, and if installing on a powerful HPC cluster, serious consideration should be given to which will be the most beneficial. For basic development and testing, however, it really doesn’t matter which is used. I use OpenMPI on my Ubuntu laptop, which can be installed with a simple:
sudo apt-get install openmpi-bin libopenmpi-dev
That’s it! You’re ready to go… You can test your installation with a simple “Hello world” program such as:
#include <stdio.h>
#include <mpi.h>
int main (int argc,char **argv)
{
int rank, size;
MPI_Init (&argc, &argv);
MPI_Comm_rank (MPI_COMM_WORLD, &rank);
MPI_Comm_size (MPI_COMM_WORLD, &size);
printf( "Hello world from process %d of %d\n", rank, size );
MPI_Finalize();
return 0;
}
You should be able to compile this with
mpicc -o helloworld helloworld.c
and run (on 2 processors) with
mpirun -np 2 helloworld
GSL
If you are writing non-trivial MCMC codes, you are almost certainly going to need to use a sophisticated math library and associated random number generation (RNG) routines. I typically use the GSL. On Ubuntu, the GSL can be installed with:
sudo apt-get install gsl-bin libgsl0-dev
A simple script to generate some non-uniform random numbers is given below.
#include <gsl/gsl_rng.h>
#include <gsl/gsl_randist.h>
int main(void)
{
int i; double z; gsl_rng *r;
r = gsl_rng_alloc(gsl_rng_mt19937);
gsl_rng_set(r,0);
for (i=0;i<10;i++) {
z = gsl_ran_gaussian(r,1.0);
printf("z(%d) = %f\n",i,z);
}
exit(EXIT_SUCCESS);
}
This can be compiled with a command like:
gcc gsl_ran_demo.c -o gsl_ran_demo -lgsl -lgslcblas
and run with
./gsl_ran_demo
SPRNG
When writing parallel Monte Carlo codes, it is important to be able to use independent streams of random numbers on each processor. Although it is tempting to “fudge” things by using a random number generator with a different seed on each processor, this does not guarantee independence of the streams, and an unfortunate choice of seeds could potentially lead to bad behaviour of your algorithm. The solution to this problem is to use a parallel random number generator (PRNG), designed specifically to give independent streams on different processors. Unfortunately the GSL does not have native support for such parallel random number generators, so an external library should be used. SPRNG 2.0 is a popular choice. SPRNG is designed so that it can be used with MPI, but also that it does not have to be. This is an issue, as the standard binary packages distributed with Ubuntu (libsprng2, libsprng2-dev) are compiled without MPI support. If you are going to be using SPRNG with MPI, things are simpler with MPI support, so it makes sense to download sprng2.0b.tar.gz from the SPRNG web site, and build it from source, carefully following the instructions for including MPI support. If you are not familiar with building libraries from source, you may need help from someone who is.
Once you have compiled SPRNG with MPI support, you can test it with the following code:
#include <stdio.h>
#include <stdlib.h>
#include <mpi.h>
#define SIMPLE_SPRNG
#define USE_MPI
#include "sprng.h"
int main(int argc,char *argv[])
{
double rn; int i,k;
MPI_Init(&argc,&argv);
MPI_Comm_rank(MPI_COMM_WORLD,&k);
init_sprng(DEFAULT_RNG_TYPE,0,SPRNG_DEFAULT);
for (i=0;i<10;i++)
{
rn = sprng();
printf("Process %d, random number %d: %f\n", k, i+1, rn);
}
MPI_Finalize();
exit(EXIT_SUCCESS);
}
which can be compiled with a command like:
mpicc -I/usr/local/src/sprng2.0/include -L/usr/local/src/sprng2.0/lib -o sprng_demo sprng_demo.c -lsprng -lgmp
You will need to edit paths here to match your installation. If if builds, it can be run on 2 processors with a command like:
mpirun -np 2 sprng_demo
If it doesn’t build, there are many possible reasons. Check the error messages carefully. However, if the compilation fails at the linking stage with obscure messages about not being able to find certain SPRNG MPI functions, one possibility is that the SPRNG library has not been compiled with MPI support.
The problem with SPRNG is that it only provides a uniform random number generator. Of course we would really like to be able to use the SPRNG generator in conjunction with all of the sophisticated GSL routines for non-uniform random number generation. Many years ago I wrote a small piece of code to accomplish this, gsl-sprng.h. Download this and put it in your include path for the following example:
#include <mpi.h>
#include <gsl/gsl_rng.h>
#include "gsl-sprng.h"
#include <gsl/gsl_randist.h>
int main(int argc,char *argv[])
{
int i,k,po; gsl_rng *r;
MPI_Init(&argc,&argv);
MPI_Comm_rank(MPI_COMM_WORLD,&k);
r=gsl_rng_alloc(gsl_rng_sprng20);
for (i=0;i<10;i++)
{
po = gsl_ran_poisson(r,2.0);
printf("Process %d, random number %d: %d\n", k, i+1, po);
}
MPI_Finalize();
exit(EXIT_SUCCESS);
}
A new GSL RNG, gsl_rng_sprng20 is created, by including gsl-sprng.h immediately after gsl_rng.h. If you want to set a seed, do so in the usual GSL way, but make sure to set it to be the same on each processor. I have had several emails recently from people who claim that gsl-sprng.h “doesn’t work”. All I can say is that it still works for me! I suspect the problem is that people are attempting to use it with a version of SPRNG without MPI support. That won’t work… Check that the previous SPRNG example works, first.
I can compile and run the above code with
mpicc -I/usr/local/src/sprng2.0/include -L/usr/local/src/sprng2.0/lib -o gsl-sprng_demo gsl-sprng_demo.c -lsprng -lgmp -lgsl -lgslcblas
mpirun -np 2 gsl-sprng_demo
Parallel Monte Carlo
Now we have parallel random number streams, we can think about how to do parallel Monte Carlo simulations. Here is a simple example:
#include <math.h>
#include <mpi.h>
#include <gsl/gsl_rng.h>
#include "gsl-sprng.h"
int main(int argc,char *argv[])
{
int i,k,N; double u,ksum,Nsum; gsl_rng *r;
MPI_Init(&argc,&argv);
MPI_Comm_size(MPI_COMM_WORLD,&N);
MPI_Comm_rank(MPI_COMM_WORLD,&k);
r=gsl_rng_alloc(gsl_rng_sprng20);
for (i=0;i<10000;i++) {
u = gsl_rng_uniform(r);
ksum += exp(-u*u);
}
MPI_Reduce(&ksum,&Nsum,1,MPI_DOUBLE,MPI_SUM,0,MPI_COMM_WORLD);
if (k == 0) {
printf("Monte carlo estimate is %f\n", (Nsum/10000)/N );
}
MPI_Finalize();
exit(EXIT_SUCCESS);
}
which calculates a Monte Carlo estimate of the integral
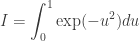
using 10k variates on each available processor. The MPI command MPI_Reduce is used to summarise the values obtained independently in each process. I compile and run with
mpicc -I/usr/local/src/sprng2.0/include -L/usr/local/src/sprng2.0/lib -o monte-carlo monte-carlo.c -lsprng -lgmp -lgsl -lgslcblas
mpirun -np 2 monte-carlo
Parallel chains MCMC
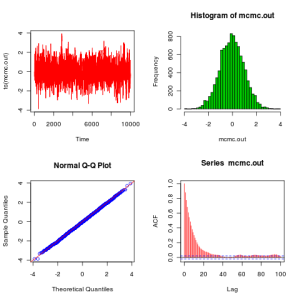
Once parallel Monte Carlo has been mastered, it is time to move on to parallel MCMC. First it makes sense to understand how to run parallel MCMC chains in an MPI environment. I will illustrate this with a simple Metropolis-Hastings algorithm to sample a standard normal using uniform proposals, as discussed in a previous post. Here an independent chain is run on each processor, and the results are written into separate files.
#include <gsl/gsl_rng.h>
#include "gsl-sprng.h"
#include <gsl/gsl_randist.h>
#include <mpi.h>
int main(int argc,char *argv[])
{
int k,i,iters; double x,can,a,alpha; gsl_rng *r;
FILE *s; char filename[15];
MPI_Init(&argc,&argv);
MPI_Comm_rank(MPI_COMM_WORLD,&k);
if ((argc != 3)) {
if (k == 0)
fprintf(stderr,"Usage: %s <iters> <alpha>\n",argv[0]);
MPI_Finalize(); return(EXIT_FAILURE);
}
iters=atoi(argv[1]); alpha=atof(argv[2]);
r=gsl_rng_alloc(gsl_rng_sprng20);
sprintf(filename,"chain-%03d.tab",k);
s=fopen(filename,"w");
if (s==NULL) {
perror("Failed open");
MPI_Finalize(); return(EXIT_FAILURE);
}
x = gsl_ran_flat(r,-20,20);
fprintf(s,"Iter X\n");
for (i=0;i<iters;i++) {
can = x + gsl_ran_flat(r,-alpha,alpha);
a = gsl_ran_ugaussian_pdf(can) / gsl_ran_ugaussian_pdf(x);
if (gsl_rng_uniform(r) < a)
x = can;
fprintf(s,"%d %f\n",i,x);
}
fclose(s);
MPI_Finalize(); return(EXIT_SUCCESS);
}
I can compile and run this with the following commands
mpicc -I/usr/local/src/sprng2.0/include -L/usr/local/src/sprng2.0/lib -o mcmc mcmc.c -lsprng -lgmp -lgsl -lgslcblas
mpirun -np 2 mcmc 100000 1
Parallelising a single MCMC chain
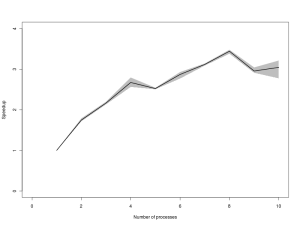
The parallel chains approach turns out to be surprisingly effective in practice. Obviously the disadvantage of that approach is that “burn in” has to be repeated on every processor, which limits how much efficiency gain can be acheived by running across many processors. Consequently it is often desirable to try and parallelise a single MCMC chain. As MCMC algorithms are inherently sequential, parallelisation is not completely trivial, and most (but not all) approaches to parallelising a single MCMC chain focus on the parallelisation of each iteration. In order for this to be worthwhile, it is necessary that the problem being considered is non-trivial, having a large state space. The strategy is then to divide the state space into “chunks” which can be updated in parallel. I don’t have time to go through a real example in detail in this blog post, but fortunately I wrote a book chapter on this topic almost 10 years ago which is still valid and relevant today. The citation details are:
Wilkinson, D. J. (2005) Parallel Bayesian Computation, Chapter 16 in E. J. Kontoghiorghes (ed.) Handbook of Parallel Computing and Statistics, Marcel Dekker/CRC Press, 481-512.
The book was eventually published in 2005 after a long delay. The publisher which originally commisioned the handbook (Marcel Dekker) was taken over by CRC Press before publication, and the project lay dormant for a couple of years until the new publisher picked it up again and decided to proceed with publication. I have a draft of my original submission in PDF which I recommend reading for further information. The code examples used are also available for download, including several of the examples used in this post, as well as an extended case study on parallelisation of a single chain for Bayesian inference in a stochastic volatility model. Although the chapter is nearly 10 years old, the issues discussed are all still remarkably up-to-date, and the code examples all still work. I think that is a testament to the stability of the technology adopted (C, MPI, GSL). Some of the other handbook chapters have not stood the test of time so well.
For basic information on getting started with MPI and key MPI commands for implementing parallel MCMC algorithms, the above mentioned book chapter is a reasonable place to start. Read it all through carefully, run the examples, and carefully study the code for the parallel stochastic volatility example. Once that is understood, you should find it possible to start writing your own parallel MCMC algorithms. For further information about more sophisticated MPI usage and additional commands, I find the annotated specification: MPI – The complete reference to be as good a source as any.