I’ve recently acquired a new laptop with an Intel i7 Quad Core CPU – an i7-940XM to be precise, and I’m interested in the possibility of running parallel MCMC codes on this machine (a Dell Precision M4500) in order to speed things up a bit. I’m running the AMD64 version of Ubuntu Linux 10.10 on it, as it has 8GB of (1333MHz DDR2 dual channel) RAM. It also contains an NVIDIA 1GB Quadro FX graphics card, which I could probably also use for GPU-style speed-up using CUDA, but I don’t really want that kind of hassle if I can avoid it. In a previous post I gave an Introduction to parallel MCMC, which explains how to set up an MPI-based parallel computing environment with Ubuntu. In this post I’m just going to look at a very simple embarrassingly parallel Monte Carlo code, based on the code monte-carlo.c from the previous post. The slightly modified version of the code is given below.
#include <math.h>
#include <mpi.h>
#include <gsl/gsl_rng.h>
#include "gsl-sprng.h"
int main(int argc,char *argv[])
{
int i,k,N; long Iters; double u,ksum,Nsum; gsl_rng *r;
MPI_Init(&argc,&argv);
MPI_Comm_size(MPI_COMM_WORLD,&N);
MPI_Comm_rank(MPI_COMM_WORLD,&k);
Iters=1e9;
r=gsl_rng_alloc(gsl_rng_sprng20);
for (i=0;i<(Iters/N);i++) {
u = gsl_rng_uniform(r);
ksum += exp(-u*u);
}
MPI_Reduce(&ksum,&Nsum,1,MPI_DOUBLE,MPI_SUM,0,MPI_COMM_WORLD);
if (k == 0) {
printf("Monte carlo estimate is %f\n", Nsum/Iters );
}
MPI_Finalize();
exit(EXIT_SUCCESS);
}
This code does 10^9 iterations of a Monte Carlo integral, dividing them equally among the available processes. This code can be compiled with something like:
mpicc -I/usr/local/src/sprng2.0/include -L/usr/local/src/sprng2.0/lib -o monte-carlo monte-carlo.c -lsprng -lgmp -lgsl -lgslcblas
and run with (say) 4 processes with a command like:
time mpirun -np 4 monte-carlo
How many processes should one run on this machine? This is an interesting question. There is only one CPU in this laptop, but as the name suggests, it has 4 cores. Furthermore, each of those cores is hyper-threaded, so the linux kernel presents it to the user as 8 processors (4 cores, 8 siblings), as a quick cat /proc/cpuinfo will confirm. Does this really mean that it is the equivalent of 8 independent CPUs? The short answer is “no”, but running 8 processes of an MPI (or OpenMP) job could still be optimal. I investigated this issue empirically by varying the number of processes for the MPI job from 1 to 10, doing 3 repeats for each to get some kind of idea of variability (I’ve been working in a lab recently, so I know that all good biologists always do 3 repeats of everything!). The conditions were by no means optimal, but probably quite typical – I was running the Ubuntu window manager, several terminal windows, had Firefox open with several tabs in another workspace, and Xemacs open with several buffers, etc. The raw timings (in seconds) are given below.
NP T1 T2 T3 1 62.046 62.042 61.900 2 35.652 34.737 36.116 3 29.048 28.238 28.567 4 23.273 24.184 22.207 5 24.418 24.735 24.580 6 21.279 21.184 22.379 7 20.072 19.758 19.836 8 17.858 17.836 18.330 9 20.392 21.290 21.279 10 22.342 19.685 19.309
A quick scan of the numbers in the table makes sense – the time taken decreases steadily as the number of processes increases up to 8 processes, and then increases again as the number goes above 8. This is exactly the kind of qualitative pattern one would hope to see, but the quantitative pattern is a bit more interesting. First let’s look at a plot of the timings.
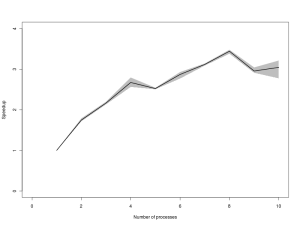
You will probably need to click on the image to be able to read the axes. The black line gives the average time, and the grey envelope covers all 3 timings. Again, this is broadly what I would have expected – time decreasing steadily to 4 processes, then diminishing returns from 4 to 8 processes, and a penalty for attempting to run more than 8 processes in parallel. Now lets look at the speed up (speed relative to the average time of the 1 processor version).
Here again, the qualitative pattern is as expected. However, inspection of the numbers on the y-axis is a little disappointing. Remeber that this not some cleverly parallelised MCMC chain with lots of inter-process communication – this is an embarrassingly parallel Monte Carlo job – one would expect to see close to 8x speedup on 8 independent CPUs. Here we see that for 4 processes, we get a little over 2.5x speedup, and if we crank things all the way up to 8 processes, we get nearly 3.5x speedup. This isn’t mind-blowing, but it is a lot better than nothing, and this is a fairly powerful processor, so even the 1 processor code is pretty quick…
So, in answer to the question of how many processes to run, the answer seems to be that if the code is very parallel, running 8 processes will probably be quickest, but running 4 processes probably won’t be much slower, and will leave some spare capacity for web browsing, editing, etc, while waiting for the MPI job to run. As ever, YMMV…
Tags: C, Dell, GSL, i7, Intel, laptop, Monte Carlo, MPI, multi-core, OpenMPI, parallel, Precision, Quad core, SPRNG
13/03/2011 at 06:11 |
great post. I have myself an I7 processor, hackintosh I built. I did a performance monte carlo MPI study, my results are very similar to the ones I see here
26/05/2011 at 05:00 |
Interesting. Did you try disabling Hyperthreading in the BIOS and running the code with 4 threads? I find that Matlab (R2011a, Ubuntu 64-bit) is a bit quicker on benchmarks with HT disabled. Wondering if that’s true in general of number crunching programs or it’s just a Matlab thing.
26/05/2011 at 08:24 |
No I didn’t disable hyperthreading, but I thought about it, as it raises some interesting issues. I’m not surprised by the results you see – I would expect to see the same with my MPI jobs – there is no point wasting time trying to cleverly hyperthread when you have 4 CPU intensive threads – it makes sense that that would slow things down. However, the other potential big difference is the “baseline” speed of one thread. Presumably one thread will run more slowly with hyperthreading disabled, which will then make the multi-threaded jobs look faster relative to 1 thread, even if they are not actually any faster than when hyperthreading is turned on… This is potentially misleading, I think. But the main reason for leaving hyperthreading turned on (other than lazyness) is the same reason I ran stuff alongside a window manager, firefox, etc. – to get some idea about real-world speed-ups, rather than theoretical speedup. Most people are going to want hyperthreading turned on, just as they want to run a window manager, and I am really interested in how much faster my code can run relative to my single process hyperthreaded job… Thanks for your feedback.
26/05/2011 at 16:41
I see. We have 4 i7s with similar configurations here and initially I had disabled HT on just one. The benchmarks looked a bit better and I didn’t see adverse consequences in everyday use (Matlab, Python, Firefox, NX and so forth), so I disabled HT on all 4 after a few months. Haven’t switched back.
25/08/2011 at 11:36 |
I’ve never used the RNGs in the GSL so sorry if this is a stupid question but how have you handled seeding the generator. Is each thread definitely getting its own, independent random number stream?
26/08/2011 at 11:54 |
In a nutshell, yes. But this functionality is not directly provided by the GSL. I’m actually using SPRNG to generate independent streams on each thread, then wrapping each one up as a GSL generator so that I can use the GSL non-uniform generation functions with the SPRNG streams. See my post on getting started with parallel MCMC for further details: http://darrenjw.wordpress.com/2010/12/14/getting-started-with-parallel-mcmc/
30/12/2011 at 15:44 |
[...] Parallel Monte Carlo with an Intel i7 Quad Core: a quick look at the potential speed-ups possible exploiting parallelisation on a laptop with a [...]