Background
Over the next few months I’m intending to have a series of posts on recent developments in MCMC and algorithms of Metropolis-Hastings type. These posts will assume a basic familiarity with stochastic simulation and R. For reference, I have some old notes on stochastic simulation and MCMC from a course I used to teach. There were a set of computer practicals associated with the course which focused on understanding the algorithms, mainly using R. Indeed, this post is going to make use of the example from this old practical. If anything about the rest of this post doesn’t make sense, you might need to review some of this background material. My favourite introductory text book on this subject is Gamerman’s Markov Chain Monte Carlo. In this post I’m going to briefly recap the key idea behind the Metropolis-Hastings algorithm, and illustrate how these kinds of algorithms are typically implemented. In order to keep things as simple as possible, I’m going to use R for implementation, but as discussed in a previous post, that probably won’t be a good idea for non-trivial applications.
Metropolis-Hastings
The motivation is a need to understand a complex probability distribution, p(x). In applications to Bayesian statistics, this distribution is usually a posterior from a Bayesian analysis. A good way to understand an intractable distribution is to simulate realisations from it and study those. However, this often isn’t easy, either. The idea behind MCMC is to simulate a Markov chain whose equilibrium distribution is p(x). Metropolis-Hastings (M-H) provides a way to correct a fairly arbitrary transition kernel q(x’|x) (which typically won’t have p(x) as its equilibrium) to give a chain which does have the desired target. In M-H, the transition kernel is used to generate a proposed new value, x’ for the chain, which is then accepted as the new state at random with a particular probability a(x’|x)=min(1,A), where A = p(x’)q(x|x’)/[p(x)q(x’|x)].
If the value is accepted, then the chain moves to the proposed new state, x’. If the value is not accepted, the chain still advances to the next step, but the new state is given by the previous state of the chain, x.
It is clear that this algorithm is also a Markov chain, and that for x’ != x, the transition kernel of this chain is q(x’|x)a(x’|x). A couple of lines of algebra will then confirm that this “corrected” Markov chain satisfies detailed balance for the target p(x). Therefore, under some regularity conditions, this chain will have p(x) as its equilibrium, and this gives a convenient way of simulating values from this target.
Special case: the Metropolis method
It is clear from the form of the acceptance probability that a considerable simplification arises in the case where the proposal kernel is symmetric, having q(x’|x)=q(x|x’). This is useful, as a convenient updating strategy is often to update the current value of x by adding an innovation sampled from a distribution that is symmetric about zero. This clearly gives a symmetric kernel, which then drops out of the acceptance ratio, to give A=p(x’)/p(x).
Example
The example we will use for illustration is a Metropolis method for the standard normal distribution using innovations from a U(-eps,eps) distribution. Below is a simple R implementation of the algorithm
metrop1=function(n=1000,eps=0.5)
{
vec=vector("numeric", n)
x=0
vec[1]=x
for (i in 2:n) {
innov=runif(1,-eps,eps)
can=x+innov
aprob=min(1,dnorm(can)/dnorm(x))
u=runif(1)
if (u < aprob)
x=can
vec[i]=x
}
vec
}
First a candidate value (can) is constructed by perturbing the current state of the chain with the uniform innovation. Then the acceptance probability is computed, and the chain is updated appropriately depending on whether the proposed new value is accepted. Note the standard trick of picking an event with probability p by checking to see if u<p, where u is a draw from a U(0,1).
We can execute this code and plot the results with the following peice of code:
plot.mcmc<-function(mcmc.out)
{
op=par(mfrow=c(2,2))
plot(ts(mcmc.out),col=2)
hist(mcmc.out,30,col=3)
qqnorm(mcmc.out,col=4)
abline(0,1,col=2)
acf(mcmc.out,col=2,lag.max=100)
par(op)
}
metrop.out<-metrop1(10000,1)
plot.mcmc(metrop.out)
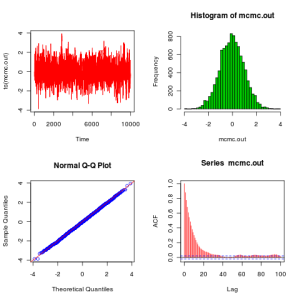
From these plots we see that the algorithm seems to be working as expected. Before finishing this post, it is worth explaining how to improve this code to get something which looks a bit more like the kind of code that people would actually write in practice. The next version of the code (below) makes use of the fact that min(1,A) is redundant if you are just going to compare to a uniform (since values of the ratio larger than 1 will be accepted with probability 1, as they should), and also that it is unnecessary to recalculate the likelihood of the current value of the chain at every iteration – better to store and re-use the value. That obviously doesn’t make much difference here, but for real problems likelihood computations are often the main computational bottleneck.
metrop2=function(n=1000,eps=0.5)
{
vec=vector("numeric", n)
x=0
oldlik=dnorm(x)
vec[1]=x
for (i in 2:n) {
innov=runif(1,-eps,eps)
can=x+innov
lik=dnorm(can)
a=lik/oldlik
u=runif(1)
if (u < a) {
x=can
oldlik=lik
}
vec[i]=x
}
vec
}
However, this code still has a very serious flaw. It computes likelihoods! For this problem it isn’t a major issue, but in general likelihoods are the product of a very large number of small numbers, and numerical underflow is a constant hazard. For this reason (and others), no-one ever computes likelihoods in code if they can possibly avoid it, but instead log-likelihoods (which are the sum of a large number of reasonably-sized numbers, and therefore numerically very stable). We can use these log-likelihoods to calculate a log-acceptance ratio, which can then be compared to the log of a uniform for the accept-reject decision. We end up with the code below, which now doesn’t look too different to the kind of code one might actually write…
metrop3=function(n=1000,eps=0.5)
{
vec=vector("numeric", n)
x=0
oldll=dnorm(x,log=TRUE)
vec[1]=x
for (i in 2:n) {
can=x+runif(1,-eps,eps)
loglik=dnorm(can,log=TRUE)
loga=loglik-oldll
if (log(runif(1)) < loga) {
x=can
oldll=loglik
}
vec[i]=x
}
vec
}
It is easy to verify that all 3 of these implementations behave identically. Incidentally, most statisticians would consider all 3 of the above codes to represent exactly the same algorithm. They are just slightly different implementations of the same algorithm. I mention this because I’ve noticed that computing scientists often have a slightly lower-level view of what constitutes an algorithm, and would sometimes consider the above 3 algorithms to be different.